Y gracias a que cada vez más películas y series de televisión van incorporando algunos de estos pequeños pero trascendentales detalles a su guión, nosotros, los "ciudadanos de a pié", estamos siendo introducidos de una forma divertida y amena en lo que es el complejo mundo de los números. Aquí os he querido hacer un listado de algunas de estas series y películas, junto con los términos matemáticos más importantes que se mencionan en cada una de ellas (con pulsar en cualquiera de ellos, os aparecerá una definición básica y la posibilidad de ampliarla en un enlace adjunto). Espero que os guste...
"21 Blackjack"
Robert Luketic (2008) EEUUEn 21 Blackjack los protagonistas indiscutibles son la EstadísticaLa Estadística es una ciencia con base matemática referente a la recolección, análisis e interpretación de datos. Es utilizada para la toma de decisiones en áreas tan diferentes como las ciencias naturales, la sociología, la medicina o el mundo de los negocios.
Simplificando mucho, lo que se hace en Estadística es tomar una muestra representativa de población y analizar los datos que proporciona dicha muestra sobre un fenómeno a estudiar, con la finalidad de predecir acontecimientos futuros.
Fuente y más información, y dentro de ella la Teoría de la Probabilidad La Teoría de la Probabilidad es la parte de la matemática que estudia los llamados fenómenos aleatorios, aquellos en los que, a pesar de realizarse el experimento en las mismas condiciones, existen varios resultados posibles (como es el caso del lanzamiento de un dado o de una moneda).
La probabilidad medirá la frecuencia con que se de un u otro resultado si se hace un experimento indefinidamente.
Fuente y más información. Sin embargo también se mencionan temas como la Paradoja de Monty HallEl Problema de Monty Hall conocido también como la Paradoja de Monty Hall, es un problema matemático de probabilidad que está inspirado por el concurso televisivo estadounidense “Let's Make a Deal” (Hagamos un trato), sin embargo tomó finalmente el nombre de su presentador, Monty Hall.
Dice lo siguiente
El concursante debe elegir una puerta entre tres (todas cerradas), y su premio consiste en llevarse lo que se encuentra detrás de la puerta elegida. Se sabe cierto que una de ellas oculta un coche, y que tras las otras dos hay una cabra. Una vez que el concursante ha elegido una puerta y le comunica al público y al presentador su elección, Monty (el presentador) abre una de las otras puertas y muestra que detrás de ella hay una cabra. En este momento se le da la opción al concursante de cambiar, si lo desea, de puerta (tiene dos opciones) ¿Debe el concursante mantener su elección original o escoger la otra puerta? ¿Hay alguna diferencia?
Hagamos un pequeño análisis probabilístico:
La probabilidad de que el concursante escoja en su primera oportunidad la puerta que oculta el coche es de 1/3, por lo que la probabilidad de que el coche se encuentre en una de las puertas que no ha escogido es de 2/3. ¿Qué cambia cuando el presentador muestra una cabra tras una de las otras dos puertas?
Una suposición errónea es que, una vez sólo queden dos puertas, ambas tienen la misma probabilidad (un 50%) de contener el coche. Es errónea ya que el presentador abre la puerta después de la elección de jugador. Esto es, la elección del jugador afecta a la puerta que abre el presentador. No es un suceso aleatorio ni inconexo.
Si el jugador escoge en su primera opción la puerta que contiene el coche (con una probabilidad de 1/3), entonces el presentador puede abrir cualquiera de las dos puertas. Además, el jugador pierde el coche si cambia cuando se le ofrece la oportunidad.
Pero, si el jugador escoge una cabra en su primera opción (con una probabilidad de 2/3), el presentador sólo tiene la opción de abrir una puerta, y esta es la única puerta restante que contiene una cabra. En ese caso, la puerta restante tiene que contener el coche, por lo que cambiando lo gana.
En resumen, si mantiene su elección original gana si escogió originalmente el coche (con probabilidad de 1/3), mientras que si cambia, gana si escogió originalmente una de las dos cabras (con probabilidad de 2/3). Por lo tanto, el concursante debe cambiar su elección si quiere maximizar la probabilidad de ganar el coche.
¿Por qué sucede esto?
Porque lo que muestra el presentador no afecta a tu elección original, sino sólo a la otra puerta no escogida. Una vez se abre una puerta y se muestra la cabra, esa puerta tiene una probabilidad de 0 de contener un coche, por lo que deja de tenerse en cuenta. Si el conjunto de dos puertas tenía una probabilidad de contener el coche de 2/3, entonces, si una tiene una probabilidad de 0, la otra debe tener una probabilidad de 2/3. La elección, básicamente, consiste en preguntarte si prefieres seguir con tu puerta original o escoger las otras dos puertas. La probabilidad de 2/3 se traspasa a la otra puerta no escogida (en lugar de dividirse entre las dos puertas restantes de modo que ambas tengan una probabilidad de 1/2) porque en ningún caso puede el presentador abrir la puerta escogida inicialmente. Si el presentador escogiese al azar entre las dos puertas con cabras (incluyendo la del concursante), abriese una de ellas y luego diese de nuevo a elegir, entonces las dos puertas restantes sí tendrían la misma probabilidad de contener el coche.
Fuente y más información, el Método de Newton-Raphson El Método de Newton - Raphson es un método para encontrar aproximaciones de los ceros o raíces de funciones de una variable.
Asume que la función f(x) es derivable sobre un intervalo cerrado [a,b]. Entonces f(x) tiene una pendiente definida y una única línea tangente en cada punto en el intervalo cerrado [a,b]. La tangente en (x0,f(x0)) es una aproximación a la curva de f(x) cerca del punto (x0,f(x0) ). En consecuencia, el cero de la línea tangente es una aproximación del cero de f(x).
En la Práctica:
Para obtener las aproximaciones de los ceros o raíces de la función f (x) empezamos calculando la primera aproximación, x1, como el cero de la línea tangente en un punto inicial x0 dado.
A continuación, calculamos la segunda aproximación, x2, como el cero de la línea tangente en la primera aproximación x1.
A partir de ahí, repitiendo el mismo proceso obtendremos cada vez mejores aproximaciones de la raíz de la función f(x).
En definitiva, el método consiste en aplicar la siguiente ecuación (ecuación de Newton-Raphson):
xn+1 = xn - f(xn)/f'(xn)
Fuente y más informacióny se hace una breve referencia histórica a la Acusación de Plagio a CauchyEn 1817 Bolzano publicó el siguiente panfleto:
”Una demostración puramente analítica de teorema que afirma que entre cada dos raíces que garantizan un resultado opuesto existe al menos una raíz real de la ecuación. “
Mientras al igual que otros trabajos de Bolzano, este panfleto suyo permaneció prácticamente ignorado durante cincuenta años, en 1823, Cauchy incluye el teorema en uno de sus cursos publicados. Diversos historiadores han defendido la idea de que lo hizo sin citar a su autor Bolzano lo que significaría que habría cometido plagio. Pero hasta hoy no hay pruebas concluyentes por lo que aún sigue abierta la discusión sobre este tema, con grandes estudiosos de uno y otro lado.
Fuente.
Muy curioso es que la tarta de cumpleaños de uno de los estudiantes de ingeniería lleve escrita con nata la Sucesión de FibonacciLa Sucesión de Fibonacci es un sucesión infinita de números naturales cuyo primer elemento es 0, el segundo es 1 y cada elemento restante es la suma de los dos anteriores: 0,1,1,2,3,5,8,13,21,34,55,...
Fuente y más información.
Además en más de una ocasión se repite una frase sacada de la clase: "Siempre hay que tener en cuenta el cambio de variableUn Cambio de Variable es una técnica empleada en matemática para resolver algunas ecuaciones o sistemas de ecuaciones de grado superior a uno, que de otra forma no sería posible resolver. Mediante este sistema se da paso a una ecuación equivalente, y, una vez resuelta, se deshace el cambio para obtener el valor de la incógnita inicial.
Fuente y más información", a propósito de la estrategia en el casino, pero también a la resolución del conflicto entre Ben y su profesor.
“Los Crímenes de Oxford”
Álex de la Iglesia (2008) España Aquí se presenta el problema del descifrado de la clave cambiante de la Máquina EnigmaLa Máquina Enigma y su Código en Wikipedia, utilizada por los nazis en sus transmisiones durante la II Guerra Mundial.
Llaman la atención el uso de escenarios geométricos como en el caso de la persecución durante el concierto, la escalera en hélice con un mosaico bajo ella.
Entre los conceptos matemáticos que se citan encontramos las Dimensiones FractalesDimensiones Fractales en Wikipedia, ecuaciones, series lógicas, etc., la Serie de FibonacciLa Serie de Fibonacci es un sucesión infinita de números naturales cuyo primer elemento es 0, el segundo es 1 y cada elemento restante es la suma de los dos anteriores: 0,1,1,2,3,5,8,13,21,34,55,...
Fuente y más información, las Imágenes EspecularesParejas de Números Especulares de las primeras cifras y la Simbólica-PitagóricaLa Simbólica-Pitagórica de los Números.
También se menciona el Principio de Indeterminación de HeisembergEn mecánica cuántica, la Relación o Principio de Indeterminación de Heisenberg (Werner Heisenberg, 1927) afirma que no se puede determinar, simultáneamente y con precisión arbitraria, ciertos pares de variables físicas (posición y momento lineal, etc...), pues por el mismo hecho de realizar la primera medida, el experimentador provoca una modificación de los datos, introduciendo un error que, por muy perfectos que sean nuestros instrumentos, es imposible de reducir a cero.
Fuente y más información al suponer que la publicación en prensa de la pauta del asesino le llevará a modificarla (el hecho de la observación influye en el comportamiento del objeto observado) y se cita el Teorema de Incompletitud de GödelLos Teoremas de la incompletitud de Gödel son dos célebres teoremas de Lógica Matemática, demostrados (¿?) por Kurt Gödel en 1930.
El primer teorema afirma que
”En cualquier formalización consistente[1] de las matemáticas que sea lo bastante fuerte para definir el concepto de números naturales, se puede construir una afirmación que ni se puede demostrar ni se puede refutar dentro de ese sistema.”
Este teorema ha dado lugar a multitud de malentendidos.
Encierra el siguiente significado: cualquier sistema que permita definir los números naturales necesariamente contiene afirmaciones que ni se pueden demostrar ni refutar.
El segundo Teorema de la Incompletitud de Gödel afirma que
”Ningún sistema consistente se puede usar para demostrarse a sí mismo."
En el contexto de la Informática los Teoremas de Gödel tienen una interpretación diferente pues en lógica de primer orden, los sistemas son recursivamente enumerables, sin embargo, no cumplen la propiedad más fuerte de ser un conjunto recursivo [2]. A nivel práctico esto implica que se puede construir un programa de ordenador que terminará por dar una demostración válida, pero no se puede construir un programa que dada una afirmación cualquiera determine si ésta es cierta o no.
[1] La consistencia lógica es una propiedad de un conjunto de axiomas. Se dice que un conjunto de axiomas es consistente si a partir de él no puede deducirse simultáneamente una proposición y su contraria.
[2] Un conjunto B es recursivo cuando su función característica toma valor 1 (cierto) para todos los elementos del conjunto, y 0 (falso) para el resto.
Fuente y más información a propósito del abismo entre lo verdadero y lo demostrable ("Cualquier enunciado puede ser válido").
Y se hace alusión a la paradoja de Wittgenstein sobre las reglas finitas: En boca del personaje Sheldon, nos recuerda que la sucesión 2, 4, 8… sería continuada con el número 16 por la gran mayoría de las personas, atendiendo al criterio de multiplicar por dos. Sin embargo, podría ser continuada por otro número. El criterio para continuar la sucesión sería entonces más complejo pero igualmente verdadero.
Por último también se recrea la demostración pública del Teorema de FermatEl Último Teorema de Fermat es uno de los teoremas más importantes en la historia de la matemática.
Dice lo siguiente:
Si n es un número entero mayor que 2 (es decir, n > 2), entonces no existen números enteros a, b y c (excepto las soluciones triviales, como a = 0 ó b = 0 ó c = 0) tales que cumplan la igualdad:
cn = an + bn
Fuente y más información, y en la escena final, el Efecto MariposaEl Efecto Mariposa es un concepto que hace referencia a la noción de sensibilidad a las condiciones iniciales dentro del marco de la Teoría del Caos. La idea es que, dadas unas condiciones iniciales de un determinado sistema natural, la más mínima variación en ellas puede generar un efecto considerablemente grande, haciendo que el sistema evolucione de formas totalmente diferentes.
El Efecto Mariposa suele expresarse tal como fue descrito originalmente en la meteorología: "El aleteo de una mariposa que vuela en la China puede producir un mes después un huracán en Texas" (¿tal vez una metáfora de la expansión económica japonesa en detrimento del capitalismo occidental?).
Einstein lo describió de este otro modo: "Hasta la más pequeña gota de rocío caída del pétalo de una rosa al suelo, repercute en la estrella más lejana".
Pero a lo que alude a fin de cuentas es a una situación donde pequeñas causas generan grandes efectos, a una situación que no podemos predecir - sabemos que el efecto puede ser muy grande, pero no podemos saber en qué consistirá, ni muchas veces cuándo, dónde o cómo ocurrirá -, a una situación de descontrol: no sólo no podemos “evitar que una mariposa aletee en la China”, sino, lo que es peor, no podemos “evitar que, de aletear, se produzca un huracán en Texas”.
Más información (Edward N. Lorenz) da la clave determinante para la interpretación y resolución de los hechos.
"La habitación de Fermat"
Fuente y más información, el pomo geométrico de la puerta, la barca llamada PitágorasPitágoras en Wikipedia y la biblioteca de obras matemáticas.
A lo largo de la película los personajes han de resolver toda una serie de acertijos que tenéis recopilados y resueltos aquí.
Se mencionan la Conjetura de GoldbachLa Conjetura de Goldbach es uno de los problemas abiertos más antiguos en matemáticas.
Afirma que:
Todo número par mayor que 2 puede escribirse como suma de dos números primos.
Por ejemplo, 4 = 2 + 2
6= 3 + 3
8 = 3 + 5
10 = 3 + 7 ,etc.
Lo que equivale a decir que "Todo número entero mayor que 5 se puede escribir como suma de tres primos".
Fuente y más información, el Teorema de FermatEl Último Teorema de Fermat es uno de los teoremas más importantes en la historia de la matemática.
Dice lo siguiente:
Si n es un número entero mayor que 2 (o sea, n > 2), entonces no existen números enteros a, b y c (excepto las soluciones triviales, como a = 0 ó b = 0 ó c = 0) tales que cumplan la igualdad:
cn = an + bn
Fuente y más información,el Teorema de Incompletitud de GödelLos Teoremas de la incompletitud de Gödel son dos célebres teoremas de Lógica Matemática, demostrados (¿?) por Kurt Gödel en 1930.
El primer teorema afirma que
”En cualquier formalización consistente[1] de las matemáticas que sea lo bastante fuerte para definir el concepto de números naturales, se puede construir una afirmación que ni se puede demostrar ni se puede refutar dentro de ese sistema.”
Este teorema ha dado lugar a multitud de malentendidos.
Encierra el siguiente significado: cualquier sistema que permita definir los números naturales necesariamente contiene afirmaciones que ni se pueden demostrar ni refutar.
El segundo Teorema de la Incompletitud de Gödel afirma que
”Ningún sistema consistente se puede usar para demostrarse a sí mismo."
En el contexto de la Informática los Teoremas de Gödel tienen una interpretación diferente pues en lógica de primer orden, los sistemas son recursivamente enumerables, sin embargo, no cumplen la propiedad más fuerte de ser un conjunto recursivo [2]. A nivel práctico esto implica que se puede construir un programa de ordenador que terminará por dar una demostración válida, pero no se puede construir un programa que dada una afirmación cualquiera determine si ésta es cierta o no.
[1] La consistencia lógica es una propiedad de un conjunto de axiomas. Se dice que un conjunto de axiomas es consistente si a partir de él no puede deducirse simultáneamente una proposición y su contraria.
[2] Un conjunto B es recursivo cuando su función característica toma valor 1 (cierto) para todos los elementos del conjunto, y 0 (falso) para el resto.
Fuente y más información y el Problema de KeplerEn matemáticas los problemas de empaquetamiento de esferas conciernen la disposición de esferas de idéntico tamaño rellenando un espacio.
Así La Conjetura de Kepler es una conjetura matemática acerca de la disposición de esferas idénticas en un espacio de tres dimensiones. En el Siglo XVII, Johannes Kepler afirmó con esta conjetura que no existe un arreglo de esferas sólidas e idénticas cuya densidad promedio [1] sea mayor a los arreglos dados por las estructuras cúbica centrada en las caras, y hexagonal compacta [2]. Y esa densidad es un poco mayor al 74%.
[1] La densidad del empaquetamiento es la proporción del espacio rellenado por las esferas. Como puede depender del volumen en que se mida, el problema trata normalmente de la densidad media mayor o asintótica, medida en un volumen lo suficientemente amplio.
[2] Las dos disposiciones de esferas más comunes son llamadas empaquetamiento cúbico centrado en caras – alternancia ABCABC... (donde A, B y C son los niveles o capas de esferas encajadas una con otra con una disposición determinada por el orden en el que se colocan las letras) - y empaquetamiento hexagonal – alternancia ABAB...-. Pero todas las combinaciones son posibles (ABAC, ABCBA, ABCBAC, etc.) En todas estas disposiciones cada esfera está rodeada por otras 12.
Fuente y más información sobre el apilamiento de esferas.
Son importantes en esta película el uso de la Lógica MatemáticaLa Lógica Matemática consiste en el estudio matemático de la lógica y en la aplicación de este estudio a otras áreas de las matemáticas. También guarda una estrecha relación con la ciencias de la computación y la lógica filosófica.
La lógica matemática estudia el conjunto de reglas capaces de generar todas las posibilidades combinatorias de un lenguaje, en relación con el modo en el que estas reglas codifican conceptos intuitivos de objetos matemáticos como conjuntos, números, demostraciones y computación.
El tradicional desarrollo de la lógica enfatizaba su centro de interés en la forma de argumentar, sin embargo la lógica matemática actual lo centra en un estudio combinatorio de los contenidos. Esto se aplica tanto a un nivel sintáctico (por ejemplo, el envío de una cadena de símbolos en lenguaje formal, a un programa compilador que lo convierte en una secuencia de instrucciones ejecutables por una máquina), como a un nivel semántico, construyendo modelos apropiados.
Fuente y más información, y los Números PrimosUn Número Primo es todo número natural que es divisible únicamente por sí mismos y por la unidad.
Aquí tenéis una tabla de Números primos del 1 al 100.000.
Fuente y más información.
Algunos matemáticos de relevancia mencionados: GaloisGalois en Wikipedia, FermatFermat en Wikipedia y HilbertHilbert en Wikipedia
"Una Mente Maravillosa"
Ron Howard (2001) EEUUEsta película está inspirada en la vida de John Forbes Nash, quien inventó una solución para juegos estratégicos no cooperativos a la que se llamó El Equilibrio de NashEl Equilibrio de Nash se define como un modo de obtener una estrategia óptima para juegos que involucren a dos o más jugadores: Si hay un conjunto de estrategias tal que ningún jugador se beneficia cambiando su estrategia mientras los otros no cambien la suya, entonces ese conjunto de estrategias y las ganancias correspondientes constituyen un Equilibrio de Nash.
Fuente y más información ( Teoría de juegosLa Teoría de Juegos es un área de la matemática aplicada. Sus investigadores estudian las estrategias óptimas así como el comportamiento previsto y observado de individuos en juegos.
Tiene aplicación a la estrategia militar, la economía, pero también a la biología y la folosofía.
Fuente y más información): durante la Guerra Fría, el propio Ejército de los EE UU adoptó tácticas basadas en estos principios.
"Pi: Fe en el Caos"
Darren Aronofsky (1998) EEUUDesde el punto de vista matemático y como su propio nombre ya indica, el principal protagonista de esta película son el Número PiPi (Π) es la relación entre las longitudes de una circunferencia y su diámetro.
Es un número irracional y una de las constantes matemáticas más importantes.
Su valor numérico, truncado a sus primeras cifras, es el siguiente:
Π ≈ 3,1415926535897932384...
Fuente y más información y la Teoría del CaosLa Teoría del Caos plantea que el mundo no sigue estrictamente el “modelo del reloj”, previsible y determinado, sino que tiene aspectos caóticos. El observador no es quien crea la inestabilidad o la imprevisibilidad con su ignorancia: éstas ya existen de por sí.
Un ejemplo típico, el clima. Podemos prever un eclipse o la aparición de un cometa con siglos de antelación, pero no el clima de la próxima semana. Ello es así porque depende de un enorme conjunto de circunstancias inciertas, que determinan por ejemplo que cualquier pequeña variación en un punto del planeta, genere en los próximos días o semanas un efecto considerable en el otro extremo de la tierra.
Fuente y más información.
Sin embargo aparecen también la Sucesión de FibonacciLa Sucesión de Fibonacci es un sucesión infinita de números naturales cuyo primer elemento es 0, el segundo es 1 y cada elemento restante es la suma de los dos anteriores: 0,1,1,2,3,5,8,13,21,34,55,...
Fuente y más información, la Espiral de ArquímedesLa Espiral de Arquímedes obtuvo su nombre del matemático siciliano Arquímedes (S. III a.C.) y se define como el lugar geométrico de un punto moviéndose a velocidad constante sobre una recta que gira sobre un punto de origen fijo, y a una velocidad también constante.
Como ejemplo, los surcos de los primeros discos de vinilo formaban una espiral de Arquímedes.
Fuente y más información (presente en conchas marinas, en los girasoles, en nuestro ADN, en el humo de un cigarrillo, en nuestras huellas dactilares o en la forma de la Vía Láctea), la historia del descubrimiento del Teorema de ArquímedesEl Teorema o Pprincipio de Arquímedes es un principio físico que afirma que un cuerpo total o parcialmente sumergido en un fluido estático, será empujado con una fuerza igual al peso del volumen de fluido desplazado por dicho objeto.
De este modo, cuando un cuerpo está sumergido en el fluido se genera una fuerza resultante de las presiones sobre la superficie del cuerpo, que actúa siempre hacia arriba a través del centro de gravedad del cuerpo, y de valor igual al peso del fluido desplazado.
Esta fuerza se mide en Newtons (en el SI) y su ecuación se describe como: Fy = m·g = ρf·V·g
Donde ρf es la densidad del fluido, V el volumen del cuerpo sumergido y g la aceleración de la gravedad.
Fuente y más información, la Razón ÁureaNúmero Áureo o Razón Áurea es el número irracional:
φ = (1 + √5) ÷2 ≈ 1,618033988749894848204586834365638...
(Se le representa con la letra griega φ (fi) en honor al escultor griego Fidias).
Se trata de un número algebraico que posee muchas propiedades interesantes y que fue descubierto en la antigüedad, no como “unidad” sino como una relación o proporción que se encuentra tanto en algunas figuras geométricas como en elementos de la naturaleza: es la distancia entre las espirales de una piña, la relación entre la cantidad de abejas macho y abejas hembra en un panal, la relación entre la distancia entre las espiras del interior espiralado de cualquier caracol, etc.
Hay personas que atribuyen cierta importancia mística a los objetos que siguen la Razón Áurea
A lo largo de la historia se la ha creído reconocer en diversas obras de arquitectura y otras artes, aunque en algunos de estos casos ha habido discrepancias por parte de matemáticos y arqueolólogos.
Fuente y más información (durante siglos, modelo de la proporción y canon de belleza), la representación de objetos de la naturaleza mediante fractales
Los Fractales son estructuras geométricas donde cada parte es una réplica del todo.Más información, el Modelado de Sistemas (la bolsa en este caso), la construcción de los primeros computadores y un concepto tan básico como el uso del Cálculo numéricoEl Cálculo Numérico es la rama de las matemáticas que se encarga de diseñar operaciones para, a través de números y reglas matemáticas sencillas, simular procesos matemáticos más complejos, y aplicarlos a procesos del mundo real.
Fuente y más información.
Otros detalles curiosos son el Juego de GoEl Go es un juego de estrategia creado en China hace más de 4.000 años. Se juega sobre un tablero de 19 intersecciones por 19, formando 361 intersecciones, con lo que el número de posiciones posibles asciende a aproximadamente 4,63×10170.
Con tal grado de complejidad lo mismo una sola partida puede acabar en 20 minutos, que llegar a durar hasta 6 horas.
Fuente y más información y la descripción de aspectos seudomatemáticos como la NumerologíaLa Numerología es el estudio de los números y de su interpretación. Es un conjunto de creencias o tradiciones que establecen una relación mística entre los números y los seres vivos.
Fuente y más información y la CábalaDe acuerdo con la tradición judía, la Cábala es la revelación de Dios recibida por Moisés a través del Arcángel Metratón, el cual se encuentra cara a cara con Dios.
La sabiduría de la Cábala se puede resumir en el “Árbol de la Vida”.
Árbol de la Vida es un diagrama de las fuerzas que operan en el Universo; una combinación de 10 esferas (enumeradas del 1 al 10) cada una de las cuales representan un atributo del Señor, y que están unidas por 22 senderos, a cada uno de los cuales le corresponde una de las 22 letras del alfabeto hebreo. Representa al Cosmos en su integridad, y a la vez, al Alma del ser humano en relación con el referido Cosmos.
Más información.
Página oficial de la película
"2001- Una Odisea del Espacio"
Basada en la novela homónima de Arthur C. Clarke. En esta película las matemáticas las encontramos en la geometría de los monolitos. Pues lo que asegura que “han sido creados por Seres Inteligentes” es precisamente su forma geométrica: cada uno de ellos un ortoedro perfecto, con la curiosidad de tener unas dimensiones exactas y, en los tres casos, proporcionales a los números 1, 4 y 9 (ancho, largo y alto respectivamente).
"El Cubo"
Vincenzo Natali (1998) CanadáUno de los atractivos que Cube puede tener para los matemáticos y los aficionados a los problemas en general es desentrañar la codificación numérica que tienen las diferentes salas cuyo análisis permite a los protagonistas hallar la salida del laberinto en el que se encuentran. - Teoría de números (factorización)Según el Teorema Funtamental de la Aritmética o Teorema de la Factorización, todo número entero mayor que 1 se puede escribir como producto de números primos.
Al proceso de búsqueda de estos números primos divisores se le denomina Factorización y a los números hallados, “factores primos”.
Por ejemplo: 490 = 7 x 7 x 5 x 2 x 1 = 72 x 5 x 2 x 1
Fuente y más información, los Números PrimosUn Número Primo es todo número natural que es divisible únicamente por sí mismos y por la unidad.
Aquí tenéis una tabla de Números primos del 1 al 100.000.
Fuente y más información y el Cubo de RubikEl Cubo de Rubik es un conocido rompecabezas cuyo objetivo es rearmar la configuración inicial de un cubo cuyas caras están divididas en cuadros de un mismo color cada una, una vez ha sido desarmada.
En el Cubo de Rubik “estándar” cada una de sus seis caras están dividida en nueve partes, 3x3x3, lo que conforma un total de 26 piezas (no hay pieza central) que se articulan entre sí.
Número de combinaciones posibles
Podemos combinar entre sí de cualquier forma todos los vértices del cubo lo que da lugar a 8! posibilidades. Con las aristas pasa lo mismo, es decir, que podemos combinarlas como se desee, lo que da lugar a 12! posibilidades, pero la permutación total de vértices y aristas debe de ser en total par, lo que nos elimina la mitad de las posibilidades. Por otra parte, podemos rotar todos los vértices como queramos salvo uno sin cambiar nada más en el cubo. La orientación del último vértice vendrá determinada por la que tengan los otros siete y esto nos crea 37 posibilidades. Igual debe ocurrir con las aristas, es decir, pues aparecen 211 posibilidades más. En total tendremos que el número de permutaciones posibles en el Cubo de Rubik es de:
(8! x 12! x 37 x 211 )/ 2 = 43.252.003.274.489.856.000
es decir, ¡cuarenta y tres trillones doscientos cincuenta y dos mil tres billones doscientos setenta y cuatro mil cuatrocientos ochenta y nueve millones ochocientos cincuenta y seis mil permutaciones!
Fuente y más información -.
La construcción es un enorme cubo, y en su interior una serie de habitaciones, también de forma cúbica, que vienen identificada por tres grupos de tres números cada uno (nueve números en total). Estos números indican si la habitación tiene o no trampas mortales, la posición relativa de la sala respecto al cubo total, y los movimientos que estos cubículos van describiendo, detalle que permitirá a los protagonistas averiguar cuándo se encuentran en la posición inicial.
Proyecto Cube: Una Introducción a la Geometría Tridimensional - RevistaSuma.es
"El Indomable Will Hunting"
Gus Van Sant (1997) EEUUNada más comenzar la película aparecen en una pizarra planteados y resueltos dos ejercicios de la Teoría de grafos
La Teoría de Grafos estudia las propiedades de los grafos. Para entender lo que es un grafo nos podemos referir a su representación gráfica: una serie de puntos o vértices, conectados entre sí por líneas o aristas.La utilidad práctica de los grafos es que permiten estudiar las interrelaciones entre unidades que interactúan entre sí.
Por ejemplo, una red de computadoras puede representarse y estudiarse mediante un grafo, en el cual los vértices representan terminales y las aristas representan conexiones (las cuales, a su vez, pueden ser cables o conexiones inalámbricas).
El primer artículo científico relativo a grafos fue escrito por el matemático suizo Leonhard Euler en 1736. Euler se basó en su artículo en el problema de los puentes de Königsberg.
La ciudad de Kaliningrado, originalmente Königsberg, es famosa por sus siete puentes que unen ambas márgenes del río Pregel con dos de sus islas. Dos de los puentes unen la isla mayor con la margen oriental y otros dos con la margen occidental. La isla menor está conectada a cada margen por un puente y el séptimo puente une ambas islas.
El problema planteaba lo siguiente: ¿es posible, partiendo de un lugar arbitrario, regresar al lugar de partida cruzando cada puente una sola vez?
Abstrayendo este problema y planteándolo con la (entonces aún básica) teoría de grafos, Euler consiguió demostrar que el grafo asociado al esquema de puentes de Königsberg no tiene solución, es decir, no es posible regresar al vértice de partida sin pasar por alguna arista dos veces.
Fuente y más información - si bien su lectura, debido a la fugacidad de su aparición, es casi imposible sin detener la imagen: Ejercicio 1
Dado un grafo, encontrar:
1 – la matriz de adyacencia A
2 – la matriz que da el número de caminos de longitud tres
3 – la función que genera los caminos de i à j
4 – la función que genera los caminos de 1 a 3Ejercicio 2
Conjunto de los árboles no isomorfos con 10 nodos SolucionesSolución al Primer Ejercicio:
Solución al Segundo Ejercicio:
Además podemos hallar detalles relacionados con Series FuncionalesUna Serie Funcional o Serie de Funciones es una función S (x) con dominio A, resultante de la suma infinita de funciones f (x): S(x) = fo(x) + f1(x) + f2(x) + ...
Fuente y más información, el Análisis de FourierEl Análisis de Fourier surgió a partir del intento del matemático francés Jean-Baptiste Joseph Fourier por hallar la solución a un problema práctico: la conducción del calor en un anillo de hierro. Demostró que se puede obtener una función discontinua a partir de la suma de funciones continuas.
A primera vista, puede parecer que el problema de analizar formas de ondas complejas representa una tarea ardua, pero si la forma de la onda es periódica, se puede representar con una precisión arbitraria, mediante la superposición de un número suficientemente grande de ondas senoidales que forman una serie armónica.
En otras palabras, según Fourier, toda función f(t) periódica de periodo P, se puede representar en forma de una suma infinita de funciones armónicas, de modo que su fórmula general es la que sigue:
Donde an y bn se denominan coeficientes de Fourier de la serie de Fourier de la función f(x).
La Serie de Fourier es una aplicación usada en muchas ramas de la Ingeniería, y una herramienta sumamente útil en la Teoría Matemática abstracta. Algunas áreas de aplicación son el análisis vibratorio, la acústica, la óptica, los sistemas de telecomunicaciones, el procesamiento de imágenes y señales, y la compresión de datos.
Fuente y más información, CombinatoriaLa Combinatoria es una rama de la Matemática que estudia colecciones finitas de objetos que satisfacen unos criterios específicos. En particular se ocupa del "recuento" de los objetos de dichas colecciones (combinatoria enumerativa), y de hecho la mayoría de los matemáticos la definiría como “el arte y ciencia de contar”, pero también de determinar si cierto objeto que satisfaga unas restricciones determinadas existe (combinatoria extremal).
Un ejemplo de pregunta combinatoria podría ser:
¿Cuántas combinaciones posibles pueden hacerse con un mazo de 52 cartas?
La respuesta es 52! O lo que es igual, el producto de todos los números naturales desde 1 al 52. Alrededor de 8,07 × 1067 combinaciones.
Fuente y más información, la Medalla FieldsLa Medalla Internacional para Descubrimientos Sobresalientes en Matemáticas conocida por el nombre de Medalla Fields (por el matemático John Charles Fields), es una distinción que concede la Unión Matemática Internacional cada cuatro años a uno o más matemáticos, siendo el mayor honor al que éstos pueden aspirar. Se instauró antes de la Segunda Guerra Mundial, ante la carencia del Premio Nobel de Matemáticas [1].
La medalla que se entrega al o a los galardonados está chapada en oro y muestra en una de sus caras la cabeza del matemático griego Arquímedes.
[1]Hay muchas teorías sobre el porqué Alfred Nobel no instauró el premio que lleva su nombre para las Matemáticas. Entre ellas por ejemplo se dice que en su juventud, Alfred Nobel compitió por el amor de una dama con un matemático ...
Sin embargo, actualmente la razón más aceptada es que Nobel, en el sentido práctico, no consideró esta ciencia importante para la vida y eligió para los “premios ramas” aquellas que a su juicio sí eran importantes para el avance de la sociedad.
Fuente y más información y la Teoría de CuerdasLa Teoría de Cuerdas es un modelo fundamental de la Física que afirma que todos los bloques de materia son en realidad expresiones de un objeto básico unidimensional extendido llamado "cuerda" o "filamento".
De acuerdo con esta propuesta, un electrón no es un "punto" sin estructura interna y de dimensión cero, sino una cuerda minúscula que vibra en un espacio-tiempo de más de cuatro dimensiones.
Un punto no puede hacer nada más que moverse en un espacio tridimensional. Sin embargo una cuerda además de moverse, puede oscilar de diferentes maneras. De acuerdo con esta Teoría, el electrón se distinguiría macroscópicamente por un modo muy concreto de oscilación, y así, si la cuerda oscila de un modo diferente, sabríamos que lo que estamos viendo no es un electrón sino un fotón, un quark, o cualquier otra partícula del modelo estándar.
Actualmente, la Teoría de Cuerdas es la candidata más prometedora para llegar a una teoría unificada o Teoría del Todo, capaz de describir todos los fenómenos ocurridos en la naturaleza debido a las cuatro fuerzas fundamentales: la fuerza gravitacional, la electromagnética y las fuerzas de interacción nuclear fuerte y débil.
Fuente y más información.
Algunos matemáticos de relevancia mencionados son: McLaurinMcLaurin en Wikipedia, Srinivasa RamanujanSrinivasa Ramanujanen Wikipedia y Godfrey H. HardyGodfrey H. Hardy en Wikipedia.
"Contact"
Robert Zemeckis (1997) EEUUEn "Contact" se plantean las Matemáticas como único lenguaje universal.Para los que la hayáis visto, es curioso que la idea de esta película ya fuera expresada por Julio Verne más de un siglo antes (solo que en su caso con los humanos como emisores del mensaje, y en versión geométrica):«… unos pocos días antes, un geómetra alemán propuso enviar una expedición científica a las estepas de Siberia. Allí, en aquellas vastas llanuras, tuvieron que describir formas geométricas enormes, dibujadas con trazos de una luminosidad cegadora, entre las cuales figuraba la proposición que se refiere al cuadrado de la hipotenusa, comúnmente llamada por los franceses el puente del asno”. Cualquier ser inteligente, dijo el geómetra, ha de poder entender el significado científico de la figura.
Los selenitas, si es que existen, nos responderán con una figura similar y, una vez establecida la comunicación, será fácil formar un alfabeto que nos permita conversar con los habitantes de la Luna.»
De la Tierra a la Luna
1865 Julio Verne Y una vez más, las premoniciones de Verne se cumplieron de forma bastante aproximada: El Teorema de Pitágoras El Teorema de Pitágoras establece que en un triángulo rectángulo, el cuadrado de la hipotenusa es igual a la suma de los cuadrados de los dos catetos.figura en el mensaje elaborado por los físicos canadienses Yvan Dutil y Stéphane Dumas, enviado el 1 de julio de 1999 desde la antena de 70 m. de diámetro del Evpatoria Deep Space Center en Ucrania, con destino a cuatro estrellas similares al Sol, situadas en direcciones donde el polvo interestelar alterará poco el mensaje durante su propagación.Salen a colación la Teoría de la SeñalLa Teoría de la Señal se ocupa de la descripción y caracterización matemática de las señales [1], así como de la transformación de señales mediante sistemas. Pone en evidencia, bajo una forma matemática cómoda, las principales características de una señal, ofreciendo los medios de analizar la naturaleza de las alteraciones experimentadas por las señales a su paso a través de bloques funcionales, generalmente dispositivos eléctricos o electrónicos.
En resumen, podemos decir que la Teoría de la Señal se ocupa del estudio de métodos para la representación analítica de las señales, la caracterización numérica de propiedades importantes de la señal y la caracterización de las propiedades transformadoras de la señal en diversos sistemas para proceso.
[1] Se define señal como una característica medible de un fenómeno observable, fenómeno la mayoría de las veces de naturaleza física; es un soporte físico que transporta o contiene información, pero no constituye la información en sí. La señal el resultado de una medida del fenómeno bajo observación.
Fuente, la Teoría de la RelatividadEn relación a la Teoría de la Relatividad me limitaré a exponeros la famosa Paradoja de los Gemelos:
“Imaginemos a dos gemelos de veinte años de edad. Uno permanece en la Tierra mientras el otro parte en una nave espacial, a la velocidad de la luz, hacia un lugar que dista treinta años luz de la Tierra. A su regreso, para el gemelo que se quedó en la Tierra habrían pasado sesenta años; en cambio, para el otro sólo unos pocos días".
Fuente y más información, y los casi inevitables Números PrimosUn Número Primo es todo número natural que es divisible únicamente por sí mismos y por la unidad.
Aquí tenéis una tabla de Números primos del 1 al 100.000.
Fuente y más información.
"Moebius"
Gustavo Mosquera (1996) ArgentinaEl campo matemático que se toca en esta película mezcla de intriga y ciencia-ficción es, como su propio nombre indica, la Cinta de Möbius
La Banda de Moebius o Cinta de Moebius es una superficie reglada [1] con una sola cara y un solo borde. Fue co-descubierta de forma independiente por los matemáticos alemanes August Ferdinand Möbius y Johann Benedict Listing en 1858. Banda o Cinta de Moebius es un objeto no orientable. lo que significa que si una persona que se desliza tumbada sobre una banda de Möbius, mirando hacia la derecha, al dar una vuelta completa aparecerá mirando hacia la izquierda. Si se parte con una pareja de ejes perpendiculares orientados, al desplazarse paralelamente a lo largo de la cinta, se llegará al punto de partida con la orientación invertida.
Por último, si se corta una cinta de Möbius a lo largo, a diferencia de una cinta normal, no se obtienen dos bandas, sino que se obtiene una banda más larga pero con dos giros. Si a ésta banda se la vuelve a cortar a lo largo, se obtienen otras dos bandas entrelazadas pero con vueltas. A medida que se van cortando a lo largo de cada una, se siguen obteniendo más bandas entrelazadas.
[1] Una superfice es reglada cuando el plano tangente para cada punto de la misma contiene una línea recta completamente contenida sobre la superficie.
Fuente y más información; también llamada Banda de Möbius - Topología
La Topología es el estudio de aquellas propiedades de los cuerpos geométricos que permanecen inalteradas por transformaciones continuas. Se interesa por conceptos como proximidad, número de agujeros, el tipo de consistencia (o textura) que presenta un objeto, por comparar objetos y clasificar entre otros múltiples atributos donde destacan la conectividad, la compacidad, y la metricidad, etc. Curiosidad:
A la Topología también se la conoce por la "Geometría de la página de chicle". Esto es debido a que está permitido doblar, estirar, encoger, retorcer, etc., los objetos, seguirán siendo topológicamente equivalentes siempre y cuando todo ello se haga sin romper ni separar lo que estaba unido, ni pegar algo que estaba separado.
Por ejemplo, un triángulo es topológicamente lo mismo que una circunferencia, ya que podemos transformar uno en otra de forma continua, sin romper ni pegar.
Pero una circunferencia no es lo mismo que un segmento, ya que habría que partirla por algún punto.
Un ejemplo más cotidiano es el plano del metro de Madrid: En él están representadas las estaciones y las líneas de metro que las unen. Pero no es geométricamente exacto. La curvatura de las líneas de metro no coincide, ni su longitud a escala, ni la posición relativa de las estaciones... Pero aun así es un plano perfectamente útil; en cierto sentido es exacto, pues representa fielmente cierto tipo de información, la única que necesitamos para decidir nuestro camino por la red de metro, la información topológica.
Fuente y más información -, con algún, algo desatinado guiño a la Termodinámica ( Móvil PerpetuoUn Móvil Perpetuo es un objeto en constante movimiento.
Parece que fue en la India el siglo XII la primera vez que surgió la idea sobre un dispositivo que pudiera poner en movimiento las máquinas sin utilizar la fuerza muscular de los hombres ni los animales, ni la del viento o del agua cayente. Sin embargo no fue hasta el siglo XIII, en las ciudades medievales europeas, que el interés por un motor universal, funcional en cualquier lugar, se hizo más práctico y la idea empezó a desarrollarse. Desde entonces hasta nuestros días, el hombre sigue aspirando a crear esta “máquina perfecta”.
Fuente y más información) y quizás incluso a la Mecánica CuánticaLa Mecánica Cuántica, conocida también como Mecánica Ondulatoria o Física Cuántica, es una de las ramas principales de la Física que explica el comportamiento de la materia.
Aunque su campo de aplicación pretende ser universal, la realidad es que tiene aplicación microscópica donde sus predicciones divergen radicalmente de la llamada Física o Mecánica Clásica, dedicada a explicar los comportamientos de la materia a nivel macroscópico.
(Para explicar el comportamiento de un electrón - microscópico, de pequeña escala -, recurriríamos a la Mecánica Cuántica. Sin embargo, si pretendemos comprender el movimiento de la Tierra alrededor del Sol - macroscópico, de gran escala -, recurriremos a la Mecánica Clásica.
Las suposiciones más importantes de la Mecánica Cuántica son las siguientes:
- La energía no se intercambia de forma continua, sino en forma de pequeños “paquetes” o cuantos.
- Al ser imposible fijar a la vez la posición y el momento de una partícula, se renuncia al concepto de trayectoria, vital en la Mecánica Clásica. En su lugar, el movimiento de una partícula queda regido por una función matemática que asigna a cada punto del espacio y a cada instante, la Probabilidad de que la partícula descrita se halle en tal posición en ese instante.
En los inicios y el desarrollo de la Mecánica Cuántica es imprescindible nombrar a físicos tan notables como Max Panck, Schrödinger, Heisenberg, Albert Einstein, Dirac, Bohr y Von Neumann
Fuente y más información.
"Star Trek: Primer Contacto"
Star Trek: First contact
Jonathan Frakes (1996) EEUU
Una vez los "Borg" han abordado el "Enterprise", para impedir que se apoderen del control de toda la nave el capitán ordena bloquear el ordenador central, tarea que “Data” lleva a cabo mediante un código de encriptación fractalLos Fractales son estructuras geométricas donde cada parte es una réplica del todo; la estructura básica se repite en diferentes escalas.
La Encriptación Fractal se aprovecha de la relación entre los Fractales y la Teoría del Caos [1]: en un Sistema Caótico, una mínima diferencia en las condiciones hace que el sistema evolucione de manera totalmente distinta. En lo que se basa la Criptografía a la hora de aplicar Fractales y sistemas caóticos para obtener métodos criptográficos, es en la esperanza de que utilizando métodos analíticos y sin conocer la clave secreta, el comportamiento caótico sea lo suficientemente difícil de predecir como para romper el código generado.
[1] La Teoría del Caos plantea que el mundo no sigue estrictamente el “modelo del reloj”, previsible y determinado, sino que tiene aspectos caóticos. El observador no es quien crea la inestabilidad o la imprevisibilidad con su ignorancia: éstas ya existen de por sí. Un ejemplo típico, el clima. Podemos prever un eclipse o la aparición de un cometa con siglos de antelación, pero no el clima de la próxima semana. Ello es así porque depende de un enorme conjunto de circunstancias inciertas, que determinan por ejemplo que cualquier pequeña variación en un punto del planeta, genere en los próximos días o semanas un efecto considerable en el otro extremo de la tierra.
Fuente y más información. Sin embargo no es solamente esta entrega de la saga la que nos ofrece guiños matemáticos. Por poner un ejemplo, también lo hace una entrega anterior, Star Trek II: La ira de Khan de 1982.
Uno de los aspectos matemáticos de esta película lo encontyramos en el mismo guión: la derrota de “Khan” se debe a su incapacidad para pensar en tres dimensionesUna Dimension es una magnitud que define un fenómeno físico., lo que da lugar a un enfrentamiento tipo submarino en el interior de la "Mutara Nebula" que resultará crucial.
El otro detalle es de índole técnica: con Star Trek II es la primera vez en la historia del cine que se utilizan técnicas fractales
Un Fractal es un objeto semi geométrico cuya estructura básica, fragmentada o irregular, se repite a diferentes escalas.A un objeto geométrico fractal se le atribuyen las siguientes características:
- Es demasiado irregular para ser descrito en términos geométricos tradicionales.
- Posee detalle a cualquier escala de observación.
- Es autosimilar (exacta, aproximada o estadísticamente).
- Su dimensión de Hausdorff-Besicovitch es estrictamente mayor que su dimensión topológica.
- Se define mediante un simple algoritmo recursivo.
Fuente y más información para crear escenarios por ordenador.Así mismo y aunque no siempre de un modo muy coherente, también la serie de la Saga nos deja algún que otro guiño: referencias al Número PiPi (Π) es la relación entre las longitudes de una circunferencia y su diámetro.
Es un número irracional y una de las constantes matemáticas más importantes.
Su valor numérico, truncado a sus primeras cifras, es el siguiente:
Π ≈ 3,1415926535897932384...
Fuente y más información, a las integralesBásicamente, una Integral es una suma de infinitos sumandos, infinitamente pequeños.
Es el proceso contrario a la derivación: Dada una función f(x), se trata de calcular otra F(x) tal que F’(x)=f(x).
Por ejemplo:
Calculemos la derivada de y = 5x -> y’= 5, la derivada de y = 5x + 3 -> y’ = 5, y la derivada de y = 5x - 2 -> y’ = 5
Según la anterior definición, podemos decir que ∫5 = 5x + 3, ó ∫5 = 5x - 2 o también ∫5 = 5.
Por ello se abrevia diciendo que ∫5 = 5x + cte.
En términos generales, ∫f(x)dx = F(x) + cte, tal que F’(x) = f(x)
El conjunto de todas las primitivas de una función se denomina Integral Indefinida. Y mientras que la integral indefinida nos da como resultado una función, la Integral Definida siempre dará como resultado un número: a diferencia de la anterior, la Integral Definida está determinada por dos "Límites de Integración" y tras realizar la integración, se sustituyen esos valores en la función dada. Su aplicación más directa es el cálculos del área de una función en un intervalo [a,b] dado:
Dada una función f(x) de una variable real x y un intervalo [a,b] de la recta real, la integral
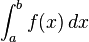
es igual al área de la región del plano xy limitada entre la gráfica de f, el eje x, y las líneas verticales x = a y x = b, donde son negativas las áreas por debajo del eje x.
Más información, el último Teorema de FermatSegún el Último Teorema de Fermat conocido también como Teorema de Fermat-Wiles
"Si n es un número entero mayor que 2 (o sea, n > 2), entonces no existen números enteros a, b y c (excepto las soluciones triviales, como a = 0 ó b = 0 ó c = 0) tales que cumplan la igualdad:
cn = an + bn"
Más información, los Puntos de LagrangeLos Puntos de Lagrange, también denominados Puntos L o Puntos de Libración, son los puntos de equilibrio del sistema en el que se mueve un cuerpo. Si nos ceñimos a un sistema solar en el que unicamente exista un sol y un planeta, encontramos que existirá un punto, llamado "de equilibrio", en el que las fuerzas gravitatorias ejercidas por el sol y el planeta sobre un cuerpo situado en ese punto, se compensan de manera que éste, en lugar de moverse en una órbita en que su posición relativa cambie continuamente, puede permanecer estable.
Más información, etc.
"Donald en el País de las Matemáticas"
Hamilton Luske (1959) EEUUSe trata de un corto producido por Walt Disney en 1959 y que nos introduce de forma muy amena en algunos aspectos simples de las matemáticas, como son las
las sumas, restas, y fracciones simples, las raíces cuadradas, el Número PiPi (Π) es la relación entre las longitudes de una circunferencia y su diámetro.
Es un número irracional y una de las constantes matemáticas más importantes.
Su valor numérico, truncado a sus primeras cifras, es el siguiente:
Π ≈ 3,1415926535897932384...
Fuente y más información, el Número ÁureoEl Número Áureo o Razón Áurea es el número irracional:
φ = (1 + √5) ÷2 ≈ 1,618033988749894848204586834365638...(Se le representa con la letra griega φ (fi) en honor al escultor griego Fidias).
Se trata de un número algebraico que posee muchas propiedades interesantes y que fue descubierto en la antigüedad, no como “unidad” sino como una relación o proporción que se encuentra tanto en algunas figuras geométricas como en elementos de la naturaleza: es la distancia entre las espirales de una piña, la relación entre la cantidad de abejas macho y abejas hembra en un panal, la relación entre la distancia entre las espiras del interior espiralado de cualquier caracol, etc.
Hay personas que atribuyen cierta importancia mística a los objetos que siguen la Razón Áurea
A lo largo de la historia se la ha creído reconocer en diversas obras de arquitectura y otras artes, aunque en algunos de estos casos ha habido discrepancias por parte de matemáticos y arqueolólogos.
Fuente y más información y las Figuras Geométricas.
“El Amor tiene Dos Caras”
The Mirror Has Two Faces
Barbra Streisand (1996) EEUUEn esta comedia romántica se mencionan los Números PrimosUn Número Primo es todo número natural que es divisible únicamente por sí mismos y por la unidad.
Aquí tenéis una tabla de Números primos del 1 al 100.000.
Fuente y más información y los Números Primos GemelosDos números primos (p, q) son Números Primos Gemelos si están separados por una distancia de 2, es decir, si q = p + 2.
Fuente y más información - del inglés "Twin Primes", aunque traducido en la película como “Números Primos Asociados”-.
“Gattaca: Un Experimento Genético”
Andrew Niccol (1997) EEUUCon esta película nos adentramos en la geometría del ADNADN – en inglés DNA – es la abreviatura de ácido desoxirribonucleico - en inglés DeoxyriboNucleic Acid -. Se localiza en el núcleo de las células y contiene la información genética que la herencia en casi todos los organismos vivos.
La parte de las Matemáticas que se ocupa del estudio de las curvas y superficies en el espacio es la Geometría Diferencial. La Geometría Diferencial es una herramienta imprescindible en el estudio del ADN, pues éste es una estructura formada por dos cadenas de nucleótidos que se enrollan formando una doble hélice a lo largo de un eje común.
Una hélice es una curva en un espacio de tres dimensiones, algo muy parecido a una escalera de caracol. Esta curva puede ser más o menos abierta y puede variar la distancia vertical que separa una de otra en función del material del que esté formada la hélice. En la estructura del ADN podríamos imaginar por tanto dos escaleras de caracol que suben en sentidos contrarios a lo largo de un eje común.
Pero en el caso del ADN, si quisiéramos adentrarnos más en su geometría, habría que especificar además que este eje no es siempre una línea recta, sino curva, y que todo el conjunto se puede retorcer en el espacio para formar una nueva hélice de orden superior, lo que se denomina “ADN sobreenrollado”.
Más información y en el Cálculo de ProbabilidadesEl Cálculo o Tería de la Probabilidad es la parte de la matemática que estudia los llamados fenómenos aleatorios, aquellos en los que, a pesar de realizarse el experimento en las mismas condiciones, existen varios resultados posibles (como es el caso del lanzamiento de un dado o de una moneda).
La probabilidad medirá la frecuencia con que se de un u otro resultado si se hace un experimento indefinidamente.
Fuente y más información con el que se trata toda información genética.
“El Código da Vinci”
Ron Howard (2006) EEUUSon importantes en esta película la Sucesión de FibonacciLa Sucesión de Fibonacci es un sucesión infinita de números naturales cuyo primer elemento es 0, el segundo es 1 y cada elemento restante es la suma de los dos anteriores: 0,1,1,2,3,5,8,13,21,34,55,...
Fuente y más información, la Razón ÁureaEl Número Áureo o Razón Áurea es el número irracional:
φ = (1 + √5) ÷2 ≈ 1,618033988749894848204586834365638...
(Se le representa con la letra griega φ (fi) en honor al escultor griego Fidias).
Se trata de un número algebraico que posee muchas propiedades interesantes y que fue descubierto en la antigüedad, no como “unidad” sino como una relación o proporción que se encuentra tanto en algunas figuras geométricas como en elementos de la naturaleza: es la distancia entre las espirales de una piña, la relación entre la cantidad de abejas macho y abejas hembra en un panal, la relación entre la distancia entre las espiras del interior espiralado de cualquier caracol, etc.
Hay personas que atribuyen cierta importancia mística a los objetos que siguen la Razón Áurea
A lo largo de la historia se la ha creído reconocer en diversas obras de pintura clásica - en particular de Leonardo Da Vinci -,arquitectura y otras artes, aunque en algunos de estos casos ha habido discrepancias por parte de matemáticos y arqueolólogos. .
Fuente y más información, y el Pentagrama o estrella de cinco puntas, todos ellos relacionados entre si:
El Pentagrama tiene como relación entre sus partes la Razón Aúrea. El cociente entre cada dos términos consecutivos de la Sucesión de Fibonacci tiene como límite la Razón Aúrea. En la película, la pista a seguir está en la obra de Leonardo da Vinci y su llave es la Sucesión de Fibonacci. Una de las escenas claves en el desenlace de la historia se desarrolla en la tumba de Isaac NewtonIsaac Newton en Wikipedia, de quien se dice que fue dignatario del Priorato de SiónEl Priorato de Sión fue fundado por Pierre Plantard en 1956 en el pueblo francés de Annemasse. Aunque se disolvió, eso sí, solamente lo que es su nombre, poco tiempo más tarde, fue revivido por su fundador intermitentemente entre 1962 y 1993.
Plantard esperaba que se convirtiera en una logia criptopolítica con influencias, pero dedicada a la restauración de la caballería y monarquía en Francia. Más tarde fue usada para promover el propio reclamo de Plantard de ser el rey correcto para Francia.
Entre 1961 y 1984 Plantard se las ingenió para darle un pedigree mítico al Priorato de Sión, proclamando que era una rama de la “Orden de Sión”, congregación religiosa fundada en el reino de Jerusalén durante la Primera Cruzada.
Fuente y más información. El protagonista - "Langdon" - desvela una pista cifrada reflexionando sobre los detalles del entierro multitudinario que se celebró en honor de este gran científico.Por último, varias veces en la película, pero decisivamente en la escena final en El Louvre, se ahunda en la simbología esotérica asociada a la Pirámide En la Cultura Maya la Pirámide, o triángulo con la punta en alto, representa la montaña, la subida al cielo, mientras que la Pirámide Invertida es el símbolo de la caverna, la entrada hacia el otro mundo lo que para ellos es el vientre de la tierra-madre, guardián de las semillas y los tesoros, al lado de los muertos, y que pueden ser el origen de una vida nueva. Así, la primera es principio masculino y activo mientras que la segunda es femenina y pasiva.
En la arquitectura egipcia, la Pirámide es un monumento sepulcral de piedra con base cuadrada. Esta estructura arquitectónica constituye una representación simbólica de alto nivel espiritual, coincidiendo con el concepto de unión, reencuentro de Tierra (cuadrado) y Cielo (punto central y axial). De la base cuadrada-material, empieza un proceso de purificación hacia arriba, hacia lo espiritual, a la quintaesencia.
Se identifica con el alcance de momentos de liberación suprema, es decir la mística concordancia entre alma individual y cósmica, la dimensión temporal limitada y la eternidad infinita.
Fuente y más informacióncomo principio masculino y la pirámide invertida como principio femenino.
"Enigma"
Michael Apted (2001) Reino UnidoBasada en la novela homónima escrita por Robert Harris, la trama principal de esta película gira en torno a los intentos de los matemáticos británicos por descifrar el código "Enigma"La Máquina Enigma y su Código en Wikipedia utilizado por los nazis para encriptar sus transmisiones durante la II Guerra Mundial.
El matemático Alan TuringAlan Turing en Wikipedia fue un personaje clave a la hora de romper su cifrado.
"Futurama"
Matt Groening (1999) EEUUEsta serie que narra las aventuras de un pizzero ("Fry") que despierta en el año 3000 tras haber sido criogenizado accidentalmente, nos ofrece a lo largo de sus episodios una gran variedad de guiños matemáticos. Al parecer esto es gracias a que varios de sus guionistas y productores tienen licenciaturas en ciencias.
Podéis echar un vistazo a las curiosidades matemáticas desgranadas en la serie en la página de "Bender Bending Rodríguez" (ver).
"Los Simpson"
Matt Groening (1989) EEUUDel mismo creador que Futurama, también en esta serie nos encontramos con numerosas curiosidades matemáticas. En esta página podéis echarles un vistazo.
Por poneros un ejemplo, los códigos numéricos ocultos escondidos a lo largo de los capítulos:
Cuando en la entradilla de cada capítulo, al pasar Marge por la caja registradora, ésta lanza un "fogonazo"... No se aprecia muy bien el precio que marca la pantalla, pero ... ¿Es un número al azar o entraña algún tipo de mensaje?
Bien, pues aunque a muchos ésto ya os sonará el dato, el número que aparece es el 847.63 y en este caso este "precio" de Maggie corresponde a una estadística que apareció en una revista, según la cual el gasto medio de manutención de un bebé durante un mes, en los EEUU, era de 847.63 dólares.
"Numb3rs"
esta serie está en el aire desde enero de 2005 en la cadena estadounidense CBS.Aprovechando el tirón de los primeros capítulos, Texas Instruments, junto a la productora CBS, y con la ayuda y el asesoramiento del National Council of Teachers of Mathematics (NCTM) (una asociación norteamericana de profesores de matemáticas) pusieron en marcha un programa educativo a través de la red con actividades basadas en los aspectos matemáticos que aparecen en los sucesivos episodios. Temas tan variados como ProbabilidadesLa Probabilidad mide con qué frecuencia ocurre algún suceso si se hace un determinado experimento indefinidamente.
Es un número que varia entre el 0 y el 1. Cuando el evento es imposible se dice que su probabilidad es 0. Cuando es 1 significa que el evento siempre es cierto, siempre tiene que ocurrir.
La Probabilidad p de que suceda un evento S de un total de n casos posibles igualmente probables es igual a la razón entre el número de ocurrencias h de dicho evento (casos favorables) y el número total de casos posibles n:
p = P{S} = h/n
Fuente y más información, InterpolaciónEl Método de Interpolación es un método científico lógico que consiste en suponer que el curso de los acontecimientos continuará en el futuro, convirtiéndose en las reglas que utilizamos para llegar a una nueva conclusión. br/>Es decir, sabemos a ciencia cierta que existen unos axiomas y éstos son extrapolables a la nueva situación.
En el subcampo matemático del análisis numérico, se denomina Interpolación a la construcción de nuevos puntos partiendo del conocimiento de un conjunto discreto de puntos.
Por ejemplo la aproximación de una función complicada por una más simple. Si tenemos una función cuyo cálculo resulta costoso, podemos partir de un cierto número de sus valores e interpolar dichos datos construyendo una función más simple. Obviamente no obtendremos los mismos valores evaluando la función obtenida que si evaluásemos la función original, si bien dependiendo de las características del problema y del método de interpolación usado la ganancia en eficiencia puede compensar el error cometido.
En todo caso, se trata de, a partir de n parejas de puntos (xk,yk), obtener una función f que verifique:
f(xk) = yk, k=1, .... ,n
Fuente y más información, Números PrimosUn Número Primo es todo número natural que es divisible únicamente por sí mismos y por la unidad.
Aquí tenéis una tabla de Números primos del 1 al 100.000.
Fuente y más información, Teoría del CaosLa Teoría del Caos plantea que el mundo no sigue estrictamente el “modelo del reloj”, previsible y determinado, sino que tiene aspectos caóticos. El observador no es quien crea la inestabilidad o la imprevisibilidad con su ignorancia: éstas ya existen de por sí.
Un ejemplo típico, el clima. Podemos prever un eclipse o la aparición de un cometa con siglos de antelación, pero no el clima de la próxima semana. Ello es así porque depende de un enorme conjunto de circunstancias inciertas, que determinan por ejemplo que cualquier pequeña variación en un punto del planeta, genere en los próximos días o semanas un efecto considerable en el otro extremo de la tierra.
Fuente y más información, Diagramas de VoronoiUn Diagrama de Voronoi es una partición del espacio en celdas, y que representa información de proximidad acerca de un conjunto de puntos u objetos.
Dada una familia finita de puntos P={pi,…,pn}, la celda de Voronoi de p1 es: V(pi)={p/d(p,pi) 〈 d(p,pk), para k ≠ i}
Es decir, la celda de Voronoi está formada por los puntos del plano que están más cerca de pi que del resto de los pk. En ocasiones, también se la llama “zona de influencia” de pi.El Diagrama de Voronoi de P={pi,…,pn} está formado por las celdas de Voronoi de cada uno de los puntos de P.
Más información, Fracciones ContinuasEn matemáticas, una Fracción Continua es una expresión de la forma:
donde a0 es un número entero y todos los demás números an son enteros positivos.
Fuente y más información, Teoría de la InformaciónLa Teoría de la Información es una rama de la teoría matemática de la probabilidad y la estadística que estudia la información y todo lo relacionado con ella: canales o medio de transmisión por el que viajan las señales portadoras de la información, compresión de datos (reducción del volumen de información a tratar), criptografía (proceso de cifrar y descifrar información), etc.
Fuente y más información, EntropíaLa definición más elemental del concepto de Entropía es el grado de desorden que tiene un sistema.
Pero en la Teoría de la Información la Entropía representa la medida de incertidumbre o duda existente ante un conjunto de mensajes, del cual va a recibirse uno solo.
Fuente y más información, CriptografíaLa Criptografía (del griego κρύπτω krypto, «oculto», y γράφω graphos, «escribir», literalmente «escritura oculta») es el arte o ciencia de cifrar y descifrar información utilizando técnicas que hagan posible el intercambio de mensajes de manera segura, de modo que sólo puedan ser leídos por las personas a quienes van dirigidos.
Fuente y más información, Teoría de JuegosLa Teoría de Juegos es un área de la matemática aplicada. Sus investigadores estudian las estrategias óptimas así como el comportamiento previsto y observado de individuos, en juegos. Tiene aplicación a la estrategia militar, la economía, pero también a la biología y la filosofía.
Fuente y más información, la famosa Paradoja de Monty HallEl Problema de Monty Hall es un problema matemático de probabilidad que está inspirado por el concurso televisivo estadounidense “Let's Make a Deal” (Hagamos un trato), ha tomado sin embargo el nombre de su presentador, Monty Hall.
Dice lo siguiente
El concursante debe elegir una puerta entre tres (todas cerradas), y su premio consiste en llevarse lo que se encuentra detrás de la puerta elegida. Se sabe con certeza que una de ellas oculta un coche, y que tras las otras dos hay una cabra. Una vez que el concursante ha elegido una puerta y le comunica al público y al presentador su elección, Monty (el presentador) abre una de las otras puertas y muestra que detrás de ella hay una cabra. En este momento se le da la opción al concursante de cambiar, si lo desea, de puerta. Le quedan dos opciones. ¿Debe el concursante mantener su elección original o escoger la otra puerta? ¿Hay alguna diferencia?
Hagamos un pequeño análisis probabilístico:
La probabilidad de que el concursante escoja en su primera oportunidad la puerta que oculta el coche es de 1/3, por lo que la probabilidad de que el coche se encuentre en una de las puertas que no ha escogido es de 2/3. ¿Qué cambia cuando el presentador muestra una cabra tras una de las otras dos puertas?
Una suposición errónea es que, una vez sólo queden dos puertas, ambas tienen la misma probabilidad (un 50%) de contener el coche. Es errónea ya que el presentador abre la puerta después de la elección de jugador. Esto es, la elección del jugador afecta a la puerta que abre el presentador. No es un suceso aleatorio ni inconexo.
Si el jugador escoge en su primera opción la puerta que contiene el coche (con una probabilidad de 1/3), entonces el presentador puede abrir cualquiera de las dos puertas. Además, el jugador pierde el coche si cambia cuando se le ofrece la oportunidad.
Pero, si el jugador escoge una cabra en su primera opción (con una probabilidad de 2/3), el presentador sólo tiene la opción de abrir una puerta, y esta es la única puerta restante que contiene una cabra. En ese caso, la puerta restante tiene que contener el coche, por lo que cambiando lo gana.
En resumen, si mantiene su elección original gana si escogió originalmente el coche (con probabilidad de 1/3), mientras que si cambia, gana si escogió originalmente una de las dos cabras (con probabilidad de 2/3). Por lo tanto, el concursante debe cambiar su elección si quiere maximizar la probabilidad de ganar el coche.
¿Por qué sucede esto?
Porque lo que muestra el presentador no afecta a tu elección original, sino sólo a la otra puerta no escogida. Una vez se abre una puerta y se muestra la cabra, esa puerta tiene una probabilidad de 0 de contener un coche, por lo que deja de tenerse en cuenta. Si el conjunto de dos puertas tenía una probabilidad de contener el coche de 2/3, entonces, si una tiene una probabilidad de 0, la otra debe tener una probabilidad de 2/3. La elección, básicamente, consiste en preguntarte si prefieres seguir con tu puerta original o escoger las otras dos puertas. La probabilidad de 2/3 se traspasa a la otra puerta no escogida (en lugar de dividirse entre las dos puertas restantes de modo que ambas tengan una probabilidad de 1/2) porque en ningún caso puede el presentador abrir la puerta escogida inicialmente. Si el presentador escogiese al azar entre las dos puertas con cabras (incluyendo la del concursante), abriese una de ellas y luego diese de nuevo a elegir, entonces las dos puertas restantes sí tendrían la misma probabilidad de contener el coche.
Fuente y más información etc.
Esta experiencia ha sido bautizada como “We all use Math everyday” (algo así como “Todos utilizamos las matemáticas diariamente”). Aquí podéis echar un vistazo a estas actividades.
“Cosmos“
Carl Sagan (Creator), David F. Oyster, Adrian Malone (1980) EEUU
Serie documental de 13 episodios que aborda temas como los orígenes de la vida, la búsqueda de vida en Marte, la composición de las estrellas y las galaxias, los viajes interestelares, los efectos de la velocidad de la luz, los peligros de la destrucción de la Tierra por la tecnología humana, la búsqueda de vida extraterrestre, etc.
Desde el punto de vista matemático mecionar como ejemplo, que narra cómo EratóstenesEratóstenes en Wikipedia en el siglo III a.C. fue capaz de medir con gran precisión el tamaño de la Tierra, la vida de KeplerLa vida de Kepler en Wikipedia, y el enunciado interpretación y aplicación de las 3 Leyes que llevan su nombre (Leyes de Kepler)
Las Leyes de Kepler fueron enunciadas por Johannes Kepler para explicar el movimiento de los planetas en sus órbitas alrededor del Sol.Aunque él no las enunció en el mismo orden, en la actualidad se numeran como sigue:
Primera Ley (1609): Todos los planetas se desplazan alrededor del Sol describiendo órbitas elípticas, estando el Sol situado en uno de los focos.
Segunda Ley (1609): El radio vector que une el planeta y el Sol barre áreas iguales en tiempos iguales.
Esta ley es equivalente a la constancia del momento angular, es decir, cuando el planeta está más alejado del Sol (afelio) su velocidad es menor que cuando está más cercano al Sol (perihelio). En el afelio y en el perihelio, el momento angular L es el producto de la masa del planeta, su velocidad y su distancia al centro del Sol.
L = m × r1 × v1 = m × r2 × v2
Tercera Ley (1618): Para cualquier planeta, el cuadrado de su período orbital (tiempo que tarda en dar una vuelta alrededor del Sol) es directamente proporcional al cubo de la distancia media con el Sol.
p2÷ r3 = K = constante
donde, P es el periodo orbital, r la distancia media del planeta con el Sol y K la constante de proporcionalidad.
Estas leyes también se aplican a otros cuerpos astronómicos que se encuentran como el sistema formado por la Tierra y la Luna, en mutua influencia gravitatoria.
Fuente y más información. Otros conceptos matemáticos destacados son el Cálculo de ErroresEl Cálculo de Errores, los Poliedros RegularesUn Poliedro Regular es un poliedro [1]: cuyas caras son polígonos regulares [2] idénticos.
Sólo existen cinco tipos posibles de poliedros regulares convexos: el tetraedro regular, el hexaedro regular o cubo, el octaedro regular, el dodecaedro regular y el icosaedro regular.
[1] Un Poliedro es una porción de espacio limitada por polígonos planos, que tiene por elementos característicos las Caras, las Aristas y los Vértices:
- Caras: son los polígonos que la limitan.
- Aristas: son los lados de las caras.
- Vértices: donde concurren tres o más caras.
[2] Un polígono es regular si todos sus ángulos son iguales y todos los lados son iguales
Fuente y más información, y como no, la ElipseLa Elipse en Wikipedia.
“El Día de la Bestia”
Álex de la Iglesia (1995) España PermutacionesPermutación, en Matemáticas, es cada una de las posibles ordenaciones de los elementos de un conjunto.
Por ejemplo, en el conjunto {1,2,3}, cada ordenación posible de sus elementos, sin que se repita ninguno de esos elemento, es una permutación. Así este conjunto tiene un total de 6 permutaciones: "1,2,3", "1,3,2", "2,1,3", "2,3,1", "3,1,2" y "3,2,1".
Fuente y más información.
"Alfred Hitchcock" en el Cine
Maestro del cine de suspense, también utilizó con frecuencia una figura matemática. Concretamente la EspiralEn matemáticas, una Espiral es una curva que se inicia en un punto central, y se va alejando progresivamente del centro a la vez que gira alrededor de él. Normalmente se define con una función que depende de dos valores:- El ángulo del punto respecto a un eje de referencia.
- Y la distancia desde este punto al punto central en base al ángulo.
Numerosos científicos han estudiado la aparición de espirales en la naturaleza encontrándolas en conchas, en la anatomía de los cuernos, los dientes y las uñas de los animales, incluso en las plantas.
Fuente y más información, y su equivalente en tres dimensiones, la HéliceLa Hélice en Wikipedia. Muy llamativa su presencia en Vértigo (1958), como podéis ver arriba, en la misma carátula de la película:
“El Enigma de Kaspar Hauser”
- Ama: Este profesor ha venido de lejos para hacerte una pregunta. Quiere ver cómo piensas, qué has aprendido en estos dos años y si puedes pensar con lógica. ¿Le responderás?
- Kaspar: Sí.
El profesor distribuye varias piezas de la vajilla sobre la mesa.
- Profesor: Kaspar, pongamos que esto es un pueblo. En el pueblo vive gente que sólo dice la verdad. Aquí hay otro pueblo. Su gente sólo dice mentiras. Hay dos caminos que van de estos pueblos al sitio en que te encuentras y tú estás en el cruce. Se acerca un hombre y quieres saber de qué pueblo procede; del pueblo de los honestos o del pueblo de los mentirosos. Ahora, para poder resolver este problema sólo puedes hacer una pregunta y sólo una. ¿Cuál es esa pregunta?
- Ama: Eso es demasiado difícil para él, ¿cómo podría saberlo? -> acertijo similar de la hab. de Fermat. pero al poco rato Kaspar sale con lo siguiente:
- Profesor: Admito que la pregunta es complicada. Si le preguntas al hombre si viene del pueblo de los honestos y es verdad, dirá que sí, honestamente sí. Pero si viene del pueblo de los mentirosos mentirá y también dirá sí. Aún así, hay una pregunta que resuelve el problema.
- Ama: Eso es muy difícil, demasiado complicado.
- Profesor: Tienes una pregunta, Kaspar, y sólo una, para resolver este problema lógico.
Se produce un largo silencio.
- Profesor: Kaspar, si no puedes pensar en la pregunta yo te la diré. Es ésta: Si tú vinieras del otro pueblo, ¿responderías "no" si yo te preguntara si vienes del pueblo de los mentirosos? Aplicando una doble negación, el mentiroso se ve forzado a decir la verdad. Esta construcción le obliga a revelar su identidad, ya ves. Esto es lo que yo llamo argumento lógico para descubrir la verdad.
- Kaspar: Bueno, sé otra pregunta.
- Profesor: ¿Sí? No hay ninguna otra pregunta según las leyes de la Lógica.
- Kaspar: Pero yo sé otra pregunta.
- Profesor: Escuchémosla entonces.
- Kaspar: Le preguntaría a ese hombre si era una rana. El hombre del pueblo de los honestos diría: "No, no soy una rana", porque dice la verdad. El hombre del pueblo de los mentirosos diría: "Sí, soy una rana", porque me está mintiendo. Así sabría de dónde procede.
- Profesor: Ésa no es una pregunta correcta.
Se ve a Kaspar muy contrariado.
- Profesor: No sirve, no puedo aceptarla como pregunta. No es lógica. La Lógica es deducción, no descripción. Lo que has hecho es describir algo, no deducirlo.
- Ama: Pero entendió su pregunta.
- Profesor: Entender es secundario. El razonamiento es lo importante.
"Ocena's 13"
L = número de ladrones
C = número de cuadros
C(caso1) = 6 ×L + 5
C(caso2) = 7 × L - 8
Igualando (caso1) y (caso2)
7 × L - 8 = 6 ×L + 5
7 × L - 6 × L = 5 + 8
Obtenemos el número de ladrones L = 13
Y reemplazando ahora L (número de ladrones) en cualquiera de los casos C (número de cuadros) obtendremos el número de cuadros:
C(caso1) = 6 × (13) + 5
C = 83
Por tanto eran 13 ladrones y 83 cuadros.
"La Jungla de Cristal III"
John McTiernan (1995) EEUUAcertijo - Sant Ebbes: “Yo a Sant Ebbes iba y conocí a un hombre con 7 mujeres, cada mujer tenía 7 sacos, cada saco 7 gatos y cada gato 7 gatitos. Gatitos, gatos, mujeres y sacos, ¿cuántos a Sant Ebbes iban. Mi teléfono es 555... y la respuesta. Llámeme en 30 segundos o morirá.” Solución En la película, tras realizar una serie de cálculos y llegan a la conclusión de que el número buscado ha de ser el 2401:
- ¡El teléfono es 5552401!. Marca.
- No, no, espera, ¡es un truco! olvidaba lo del hombre. Ha dicho ¿cuántos a Sant Ebbes iban, no? El acertijo empieza "Yo a Sant Ebbes iba y conocí a un hombre con...", el tío y las mujeres no iban a ninguna parte.
- ¿Y quién iba entonces?
- ¡Sólo Simon! marca un uno.
- ¿Y cómo marco un uno?
- 5550001
Ésta es pues la respuestaAcertijo - Las Garrafas de Agua: "Debería haber 2 garrafas en la fuente, una de 5 y otra de 3 galones. Llene una de ellas con 4 galones y póngala sobre la báscula. El contador (de la bomba) se parará. Sea exacto, una onza de más o de menos provocará la detonación. Si sigue vivo dentro de 5 minutos, volveremos a hablar." Solución El procedimiento que utilizaron los personajes de la Película fue llenar la garrafa de 5 galones y vaciar el contenido en la de 3. Esto deja 2 galones en la garrafa grande. A continuación vaciar la garrafa de 3 galones y rellenar con los 2 galones que teníamos en la de 5. Rellenar la garrafa de 5 galones y verter el contenido en la garrafa de 3 galones, hasta que ésta quede llena. Llegados a este punto tenderemos exactamente 4 galones en la garrafa de 5, con lo cual se podría desactivar la bomba.
Sin embargo hay más de una solución a este acertijo. Observa que en definitiva se trata de expresar el número 4 utilizando los números 3 y 5. ¿Cómo conseguirlo?
Desde un punto de vista matemático, existen tantas formas de obtener 4 galones a partir de medidas de 3 y 5 galones, como expresiones de la forma 3a + 5b = 4, siendo a y b valores enteros. A nada que nos fijemos, nos daremos cuenta de que uno de los dos coeficientes anteriores debe ser negativo, el otro positivo y ninguno de los dos nulo. Podemos asociar a la idea de "valor positivo" el número de veces que debe llenarse la garrafa correspondiente, y al "valor negativo", las veces que la otra garrafa debe vaciarse.
Supongamos por ejemplo que a = 3 y b = -1. Esto significaría que llenamos 3 veces la garrafa de capacidad 3 galones, para cuando vaya llenándose volcar su contenido en la de 5 galones, y la de 5, la vaciamos 1 única vez cuando esté llena.
En efecto, comenzamos llenando el recipiente de 3 galones y volcamos su contenido en el de 5. Volvemos a llenar la garrafa de 3 y echamos en la de 5 hasta llenarla (una vez llena tendrá 5 galones). Vaciamos la de 5 (esto responde al b = -1); en la de 3 galones quedó 1 galón que echamos en la de 5. Finalmente volvemos a llenar la garrafa de 3 galones (con lo que completamos el a = 3) y echamos su contenido en la de 5, conteniendo entonces ésta 1 + 3 = 4 galones.
Obsérvese que el procedimiento utilizado por los personajes de la Película responde a los valores a = -2 y b = 2.
"La Jungla de Cristal 4.0"
Len Wiseman (200) EEUUAcertijo - Relojes de Arena: John McClane debe desactivar una bomba nuclear a patadas. Son las 9 de la noche y McClane sabe que debe comenzar a patear la bomba a las 9:09, pero el malvado General Mohamed Montoya Stolyssnaya simplemente le ha proporcionado un reloj de arena de 4 minutos y otro de 7.
¿De qué forma puede medir McClane los nueve minutos, en los que debe contener el poder de su pierna, con los relojes de arena?Este acertijo, aunque formulado de un modo algo distinto, también aparece en la película “La Habitación de Fermat“, junto al de “La secuencia de números“, “Los unos y ceros“, “Tres cajas de caramelos”, “Las tres llaves de luz”, “Las dos puertas”, “Las hijas del Profesor Otto”, “Lecheras vecinas” y “Una cuestión de edades“, todos ellos recogidos y resueltos en una entrada anterior (ver).
Aún así, aquí tenéis otra vez la Solución. Se le dan la vuelta a ambos a la vez. Termina el de 4′ e inmediatamente se le vuelve a dar la vuelta. Cuando termina el de 7′, lo mismo. Al terminar por segunda vez el de 4 (Minuto 8), habrá pasado un minuto de arena (de la “2ª vuelta”) en el de 7′. Se le das la vuelta para que pase ese minuto y en total se habrán cumplido 9.Entradas relacionadas:
Los Enigmas de "La Habitación de Fermat"
Curiosidades Matemáticas
mamma mía!! IM-PRE-SIO-NAN-TE!! No dejas de sorprenderme... No he leído todo, pero prometo ir pinchando en las definiciones que has incluído de los teoremas y teorías, muy interesante, sí señorita... Besazo!!
ResponderEliminardesde MOR